Investigation on quantum Darwinism published in Physical Review X

In their recent study, "Classifying two-body Hamiltonians for Quantum Darwinism" [Phys. Rev. X 14, 041064 (2024)], Emery Doucet and Sebastian Deffner elucidate constraints on systems with two-body interactions to exhibit quantum Darwinism. The work serves as a guide on how the fuzzy, probabilistic quantum world gives way to the robust, objective, classical reality we experience in daily life.

What is Quantum Darwinism?

In the context of the measurement problem, decoherence explains how coherent superpositions $\sum_k c_k |s_k\rangle$ of a quantum system decay into mere classical mixtures $\rho_S=\sum_k |c_k|^2|s_k\rangle\langle s_k|$ of so-called pointer states $|s_k\rangle$ due to interactions with the environment. 

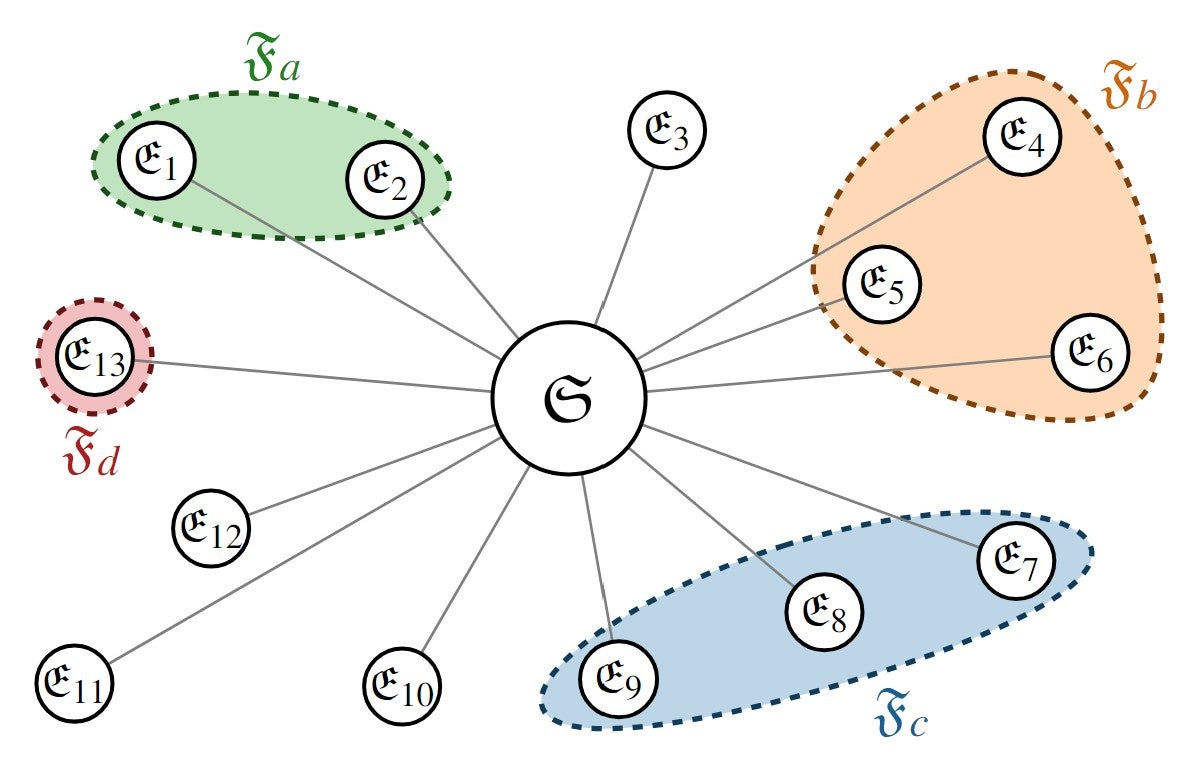
Quantum Darwinism goes one step further, trying to explain how an objective classical reality can arise from the fundamental quantum evolution in the sense that several observers agree about the state of the system. Objective properties (like an electron's position) can appear when the environment redundantly copies information about a quantum system's state into many of its degrees of freedom (fragments). A corresponding ideal "singly-branching" state takes the form

$$ |\psi\rangle = \sum_k c_k |s_k \rangle_{\mathcal{S}}\otimes |e_{k} \rangle_{\mathcal{E}_1}\otimes |e_{k} \rangle_{\mathcal{E}_2}\otimes \cdots \otimes|e_{k} \rangle_{\mathcal{E}_N}. $$

Here, the environment consists of $N$ subsystems $\mathcal{E}_n$ with orthonormal states $|e_{k} \rangle_{\mathcal{E}_n}$ .

Criteria for quantum Darwinism

1) The redundancy criterion of quantum Darwinism requires that any small fragment $\mathcal{F}$ (a small subset of the environment subsystems $\mathcal{E}_n$) has acquired almost all the information about the system $\mathcal{S}$. Mathematically, this implies that the corresponding mutual information $\mathcal{I}(\mathcal{S}:\mathcal{F})$ should be close to the system entropy $S(\rho_\mathcal{S})=-\operatorname{Tr}(\rho_\mathcal{S}\log \rho_\mathcal{S})$, i.e.,

$$\mathcal{I}(\mathcal{S}:\mathcal{F})=S(\rho_\mathcal{S})+S(\rho_\mathcal{F})-S(\rho_\mathcal{SF}) \approx  S(\rho_\mathcal{S}),$$

where $\rho_\mathcal{X}$ denotes the reduced density matrix of subsystem $\mathcal{X}$. For an ideal singly-branching state $|\psi\rangle$, we would have $\mathcal{I}(\mathcal{S}:\mathcal{F})=S(\rho_\mathcal{S})$ for any fragment size $0< |\mathcal{F}|<N$. In real quantum Darwinian systems, redundancy is signaled by a characteristic "classical plateau" of $\mathcal{I}(\mathcal{S}:\mathcal{F})$ when plotted as function of the fragment size.

2) The second citerion of objectivity for strong quantum Darwinism requires that the retrieved system information is classical in the sense that $\mathcal{I}(\mathcal{S}:\mathcal{F})\approx S(\rho_\mathcal{S})$ is close to the classical correlation $C(\rho_\mathcal{SF})$, i.e., the maximum amount of correlation that can be extracted via a local measurement on any (small) fragment. This implies that all the information about the system $\mathcal{S}$ that is redundantly encoded in any such fragment $\mathcal{F}$ is accessible via simple, non-invasive, classical measurements on $\mathcal{F}$.

Quantitative tests of quantum Darwinism

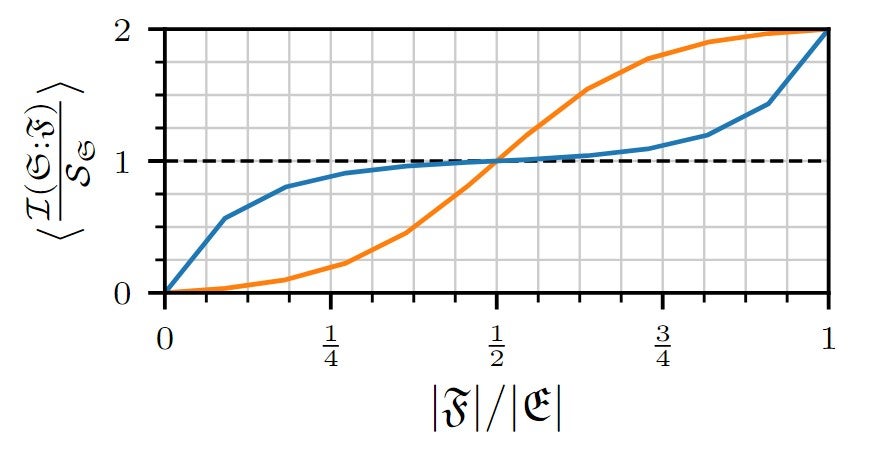In their work, Doucet and Deffner numerically probed the redundancy criterion for various small quantum systems coupled to an environment of several qubits via two-body interactions. Indeed, they found classical plateaus in the mutual information $\mathcal{I}(\mathcal{S}:\mathcal{F})$ for many natural scenarios.  In particular, singly-branching states should be preserved. This is the case if the joint system-environment dynamics does not induce any information scrambling in the environment, which would disperse the system information encoded into the environment in such a way that it can no longer be recovered by measurements of environment fragments. Sufficient mathematically constraints can be formulated as commutation relations between the system operators entering the Hamiltonian.

Unfortunately, there is no know efficient method for computing the amount of classical correlation $C(\rho_\mathcal{SF})$ such that the objectivity criterion is generally difficult to test.

The paper concludes that quantum Darwinism is the generic outcome of weak system-environment interactions. In other words, the conditions for classical objectivity are not special exceptions but rather the rule in the quantum world. The study also highlights how environmental fragments that interact symmetrically with the system tend to favor Darwinistic behavior.