The Joint Quantum Institute (JQI) is a collaboration between the University of Maryland, the National Institute of Standards and Technology (NIST), and the Laboratory for Physical Sciences (LPS), fostering interdisciplinary research at the intersection of atomic, molecular, and optical physics, condensed matter physics, and quantum information science to advance quantum technology and its applications, such as quantum computing and ultra-precise sensors.

On Monday, QLab's Dr. Thomas Barthel gave a JQI seminar, presenting a new approach to simulate strongly-correlated quantum matter efficiently on quantum computers using entanglement renormalization—a method that leverages a clever parametrization of quantum many-body states in terms of hierarchical tensor networks.

For strongly-correlated systems, like high-temperature superconductors or spin liquids, perturbative and mean-field-type approximatios break down.  A very interesting approach, motivated by real-space renormalization group, is the multi-scale entanglement renormalization ansatz (MERA). While MERA tensor networks capture important properties of the relevant many-body ground states and properly parametrize the associated corner of the Hilbert space explored by nature, they have high classical computation costs. This limits the attainable approximation accuracy [1]. To avoid the classically expensive contractions of high-order tensors, Barthel and his team have developed a variational quantum eigensolver (VQE) based on MERA and tensor Trotterization [2]. Due to its causal structure and noise-resilience, the MERA VQE can be implemented on noisy intermediate-scale quatum (NISQ) devices and still describe large physical systems. The number of required qubits is system-size independent and only grows logarithmically when using quantum amplitude estimation to speed up gradient evaluations. Translation invariance can be used to make the time complexity square-logarithmic in the system size and describe the thermodynamic limit. Results of benchmark simulations for various critical spin models and algorithmic phase diagrams substantiate a quantum advantage [3]. Furthermore, Barthel and his collaborator Qiang Miao rigorously proved the absence of "barren plateaus," a major problem in quantum optimization that can cause the training of quantum algorithms to stall [4-6].

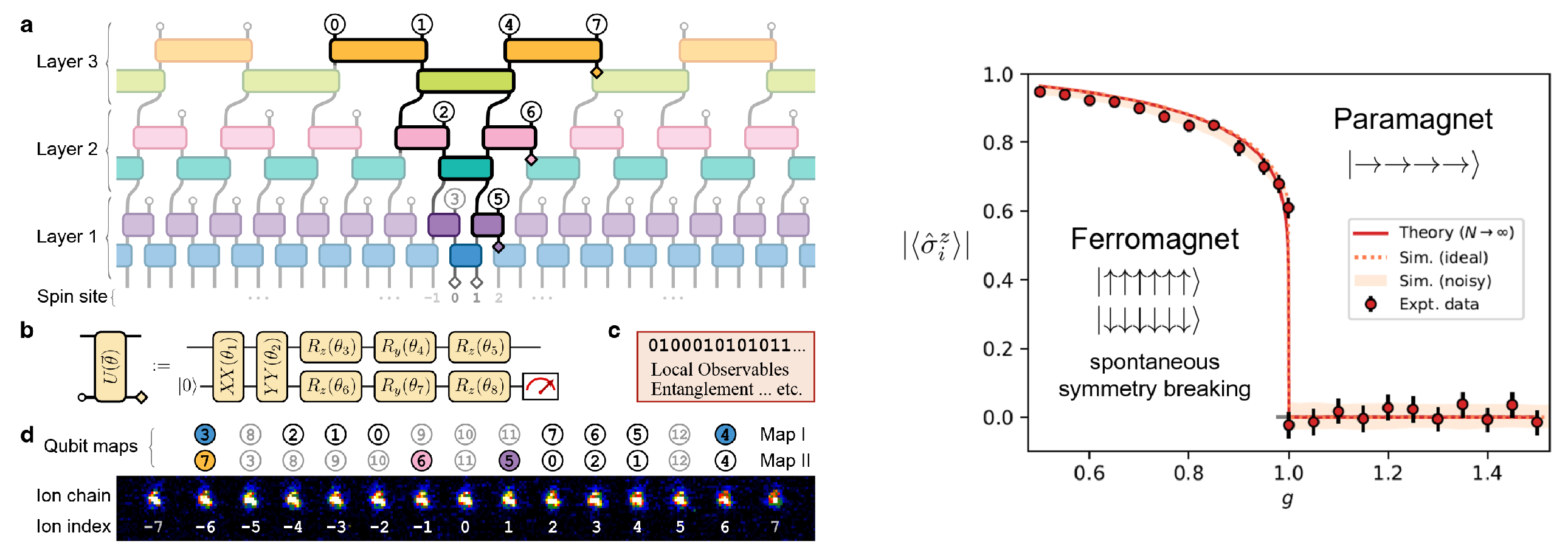
In the JQI seminar, Barthel also described first experimental tests conducted on ion-trap devices in collaboration with Marko Cetina and Ken Brown of the Duke Quantum Center, which clearly demonstrate a continuous quantum phase transition with a sharp onset of the order parameter at the critical point. Using a new holographic tomography scheme, the team was furthermore able to resolve for the first time the transition from area-law to log-area law scaling of groundstate entanglement entropies when approaching criticality [7]. This observation is a significant milestone on the way to the efficient investigation of quantum matter on quantum computers, with the long-term goal of predicting the properties of strongly-correlated systems like high-Tc materials, topologically ordered systems, and lattice QCD.

[1] "Scaling of contraction costs for entanglement renormalization algorithms including tensor Trotterization and variational Monte Carlo", PRB 111, 045104 (2025)
[2] "A quantum-classical eigensolver using multiscale entanglement renormalization", PRR 5, 033141 (2023)
[3] "Convergence and quantum advantage of Trotterized MERA for strongly-correlated systems", Quantum 9, 1631 (2025)
[4] "Absence of barren plateaus and scaling of gradients in the energy optimization of isometric tensor network states", Commun. Math. Phys. 406, 86 (2025)
[5] "Isometric tensor network optimization for extensive Hamiltonians is free of barren plateaus", PRA 109, L050402 (2024)
[6] "Equivalence of cost concentration and gradient vanishing for quantum circuits: An elementary proof in the Riemannian formulation", Quantum Sci. Technol. 9, 045039 (2024)
[7] "Probing entanglement scaling across a quantum phase transition on a quantum computer", arXiv:2412.18602